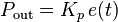CONTROL SYSTEM: 2015

P I D CONTROLLER

Proportional-integ/ral-derivative controller (PID controller) is a control loop feedback mechanism (controller) widely used in industrial control systems. A PID controller calculates an error value as the difference between a measured process variable and a desired setpoint. The controller attempts to minimize the error by adjusting the process through use of a manipulated variable.
Three separate constant parameters, and is accordingly sometimes called three-term control the proportional, the integral and derivative values, denoted P, I, and D.

What is a Propotional?

Produces an output value that is proportional to the current error value. The proportional response can be adjusted by multiplying the error by a constant K_p, called the proportional gain constant.
The proportional term is given by:

P_{\mathrm{out}}=K_p\,{e(t)}

A high proportional gain results in a large change in the output for a given change in the error.
If the proportional gain is too high, the system can become unstable (see the section on loop tuning). In contrast, a small gain results in a small output response to a large input error, and a less responsive or less sensitive controller.
If the proportional gain is too low, the control action may be too small when responding to system disturbances.
Tuning theory and industrial practice indicate that the proportional term should contribute the bulk of the output change.

What is a Integral ?

The contribution from the integral term is proportional to both the magnitude of the error and the duration of the error.
The integral in a PID controller is the sum of the instantaneous error over time and gives the accumulated offset that should have been corrected previously.
The accumulated error is then multiplied by the integral gain ( 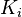$K_i$ ) and added to the controller output.
The integral term is given by:

I_{\mathrm{out}}=K_{i}\int_{0}^{t}{e(\tau)}\,{d\tau}

The integral term accelerates the movement of the process towards setpoint and eliminates the residual steady-state error that occurs with a pure proportional controller.
The integral term responds to accumulated errors from the past, it can cause the present value to overshoot the setpoint value.

What is Derivative ?

The process error is calculated by determining the slope of the error over time and multiplying this rate of change by the derivative gain K_d.

The derivative term is given by:

D_{\mathrm{out}}=K_d\frac{d}{dt}e(t)

Derivative action predicts system behavior and thus improves settling time and stability of the system.

An ideal derivative is not causal, so that implementations of PID controllers include an additional low pass filtering for the derivative term, to limit the high frequency gain and noise.

Derivative action is seldom used in practice though by one estimate in only 25% of deployed controllers because of its variable impact on system stability in real-world applications.

The magnitude of the contribution of the derivative term to the overall control action is termed the derivative gain, K_d.

1)Hubungan antara keluaran dan ralat adalah linear.

2)Nilai julat ralat untuk 0% ke 100% keluaran pengawal dinamakan ruang berkadaran atau propotional.

Keburukkan kawalan berkadaran.

1)Wujudnya offset dalam mencapai kestabilan.

2)Offset ini boleh dikurangkan dengan memberikan nilai gandaan yang tinggi.

Kebaikkan pengawal kamilan.

Boleh mengatasi offset yang didapati dalam kawasan berkadaran.
Dapat mengawal sekiranya sistem tersebut terdapat perubahan pada beban.

Keburukkan pengawal kamilan

Hanya sesuai digunakan pada suatu sistem yang mempunyai perubahan yang besar.

P+I CONTROLLER

PI controller will eliminate forced oscillations and steady state error resulting in operation of on-off controller and P controller respectively.
However, introducing integral mode has a negative effect on speed of the response and overall stability of the system.
Thus, PI controller will not increase the speed of response. It can be expected since PI controller does not have means to predict what will happen with the error in near future. This problem can be solved by introducing derivative mode which has ability to predict what will happen with the error in near future and thus to decrease a reaction time of the controller.
PI controllers are very often used in industry, especially when speed of the response is not an issue.
P+I EQUATION

P+D CONTROLLER
In general it can be said that P controller cannot stabilize higher order processes.
For the 1st order processes, meaning the processes with one energy storage, a large increase in gain can be tolerated. Proportional controller can stabilize only 1st order unstable process. Changing controller gain K can change closed loop dynamics. A large controller gain will result in control system with:
a) smaller steady state error, i.e. better reference following
b) faster dynamics, i.e. broader signal frequency band of the closed loop
system and larger sensitivity with respect to measuring noise
c) smaller

P+I+D CONTROLLER
PID controller has all the necessary dynamics: fast reaction on change of the controller input (D mode), increase in control signal to lead error towards zero (I mode) and suitable action inside control error area to eliminate oscillations (P mode).
Derivative mode improves stability of the system and enables increase in gain K and decrease in integral time constant Ti, which increases speed of the controller response.
PID controller is used when dealing with higher order capacitive processes (processes with more than one energy storage) when their dynamic is not similar to the dynamics of an integrator (like in many thermal processes). PID controller is often used in industry, but also in the control of mobile objects (course and trajectory following included) when stability and precise reference following are required. Conventional autopilot is for the most part PID type controllers.

CONCLUSION OF CONTROLLER
the conclusion of our group members can identify the pros and cons of the system in addition to learning the basics of control and recognize what was the basic controls

CHAPTER 1:INTRODUCTION TO CONTROL SYSTEM

1.0 What is a control system?

A control system is an interconnection of components forming a system configuration that will provide a desired system response.A component or process to be controlled is represented by a block.The input-output relationship represents the cause-and-effect relationship of the process.

Depending on the system configuration, there are two kinds of control systems
1)Open-loop control system
2)Closed-loop control system

1.1What Is the Meaning of Open Loop System?

An open-loop system, also known as an open-loop controller or a non-feedback controller, is a kind of system that bases the input or start of the system without taking into consideration outside factors directly caused by the system itself. In other words, the feedback caused by the system does not factor into the decision of whether or not the system runs.

Benefits of an open-loop system are often the small amount of cost associated with running the processes. It is simpler and more cost effective in most cases simply to start a repetitive process without worrying about factoring in feedback. For example, a process of a conveyor belt works more effectively without having to input feedback of the weight of every specific box that it is conveying. In this case, there is no need for feedback to be taken into consideration.

1.3 Open Loop System:

Advantages:

Simplicity and stability: they are simpler in their layout and hence are economical and stable too due to their simplicity.
Construction: Since these are having a simple layout so are easier to construct.

Disadvantages:

Accuracy and Reliability: since these systems do not have a feedback mechanism, so they are very inaccurate in terms of result output and hence they are unreliable too.
Due to the absence of a feedback mechanism, they are unable to remove the disturbances occurring from external sources.

One example of an open-loop system is a sprinkler system that turns on every day at a pre-programmed time. No matter the moisture level of the grass, the sprinkler system will continue to water it at a prescribed time. (For example, even if there was a heavy rain and the sprinklers do not need to be turned on, they will still water at their pre-programmed time.) That is an open-loop because the sprinklers will turn on no matter the feedback (in this case, the grass moisture). However, if someone were to install a moisture detector where the sprinklers only turn on once it reaches a certain point, then the entire system turns into a closed-loop system.

1.5 Open-loop Drying System

FIGURE 1: BLOCK DIAGRAM OF OPEN-LOOP SYSTEM

The opposite of an open-loop system is a closed-loop system. This is a system where the feedback of the process determines the next part of the process. For example, if there is a light that turns on in a room if motion is detected in the room, then that is a closed-loop system since the process of turning on the light entirely depends on feedback, in this case the introduction of motion.

A Closed-loop Control System, also known as a feedback control system is a control system which uses the concept of an open loop system as its forward path but has one or more feedback loops (hence its name) or paths between its output and its input. The reference to "feedback", simply means that some portion of the output is returned "back" to the input to form part of the systems excitation.

Closed-loop systems are designed to automatically achieve and maintain the desired output condition by comparing it with the actual condition. It does this by generating an error signal which is the difference between the output and the reference input. In other words, a "closed-loop system" is a fully automatic control system in which its control action being dependent on the output in some way.

1.7 Closed Loop System:

Advantages:

Accuracy: They are more accurate than open loop system due to their complex construction. They are equally accurate and are not disturbed in the presence of non-linearities.
Noise reduction ability: Since they are composed of a feedback mechanism, so they clear out the errors between input and output signals, and hence remain unaffected to the external noise sources.

Disadvantages:

Construction: They are relatively more complex in construction and hence it adds up to the cost making it costlier than open loop system.

Since it consists of feedback loop, it may create oscillatory response of the system and it also reduces the overall gain of the system.

Stability: It is less stable than open loop system but this disadvantage can be striked off since we can make the sensitivity of the system very small so as to make the system as stable as possible.

1.8 Closed-loop Control

FIGURE 3: CLOSED LOOP BLOCK DIAGRAM

1.9 Advantages and disadvantages of open loop and Closed-Loop control System.

Open Loop	Closed Loop
1. Such systems are simple in construction.	1. Accuracy of such system is always very high because controller modifies and manipulates the actuating signal such that error in the system will be zero
2. Very much convenient when output is difficult to measure.	2. Such systems senses environmental changes, as well as internal disturbances and accordingly modifies the error.
3. Such systems are easy from maintenance point of view.	3. In such system, there is reduced effect of nonlinearities and distortions.
4. Generally these are not troubled with the problems of stability.	4. Bandwidth of such system i.e. operating frequency zone for such system is very high
5. Such systems are simple to design and hence economical.

1.9.1 Differentiate between open loop and closed loop control system

Open Loop	Closed Loop
1. Any change in output has no effect on the input i.e. feedback does not exists.	1. Changes in output, affects the input which is possible by use of feedback
2. Output measurement is not required for operation of system	2. Output measurement is necessary
3. Feedback element is absent	3.Feedback element is present
4.Error detector is absent	4. Error detector is necessary
5. It is inaccurate and unreliable	5. Highly accurate and reliable
6. Highly sensitive to the disturbances	6. Less sensitive to the disturbances
7. Highly sensitive to the environmental changes	7. Less sensitive to the environmental changes
8. Bandwidth is small	8. Bandwidth is large
9. Simple to construct and cheap	9. Complicated to design and hence costly
10.Generally are stable in nature	10. Stability is the major consideration while designing
11. Highly effected by nonlinearities	11. Reduced effect of nonlinearities

1.9.2 The disadvantages of open loop and closed loop control systems are:

Open Loop	Closed Loop
1. Such systems are inaccurate and unreliable because accuracy of such systems are totally dependent on the accurate pre calibration of the controller.	1. Such systems are complicated and time consuming from design point of view and hence costlier.
2. Such systems give inaccurate results if there are variations in the external environment i.e. such systems cannot sense environmental changes.	2. Due to feedback, system tries to correct the error time to time. Tendency to over correct the error may cause oscillations without bound in the system. Hence system has to be designed taking into consideration problems of instability due to feedback. The stability problems are severe and must be taken care of while designing the system.
3. Similarly they cannot sense internal disturbances in the system, after the controller stage.
4. To maintain the quality and accuracy, recalibration of the controller is necessary, time to time.

1.9.4Automatic Control System

An automatic control system is a preset closed-loop control system that requires no operator action.This assumes the process remains in the normal range for the control system. An automatic control system has two process variables associated with it: a controlled variable and a manipulated variable.

A controlled variable is the process variable that is maintained at a specified value or within a specified range. In the previous example, the storage tank level is the controlled variable.

A manipulated variable is the process variable that is acted on by the control system to maintain the controlled variable at the specified value or within the specified range. In the previous example, the flow rate of the water supplied to the tank is the manipulated variable.

Functions of Automatic Control

In any automatic control system, the four basic functions that occur are:

i)Measurement

ii)Comparison

iii)Computation

iv)Correction

In the water tank level control system in the example above, the level transmitter measures the level within the tank. The level transmitter sends a signal representing the tank level to the level control device, where it is compared to a desired tank level.The level control device then computes how far to open the supply valve to correct any level control device correct any difference between actual and desired tank levels.

Elements of Automatic Control

The three functional elements needed to perform the functions of an automatic control system are a measurement element.An error detection element is a final control element.

Introduction to Control Process System

Concept control system
-To sense deviation of the output from the desired value and correct it, till the desired output is achiev.

Controllers are the controlling element of a control loop

- element which accepts the error in some form and decided the proper corrective action.Their function is to maintain a process variable (pressure, temperature, level..) at some desired value

Plant
System- system or process through which a particular quantity or condition is controlled. This is also called the controlled system

Controller

- control elements are components needed to generate the appropriate control signal applied to the plant

Feedback elements
- components needed to identify the functional relationship between the feedback signal and the controlled output.

Reference point
- external signal applied to the summing point of the control system cause the plant to produce a specified action. This signal represents the desired value of a controlled variable and it also called “set point.”

Controlled output
- quantity or condition of the plant which is controlled. This signal represents the controlled variable.

Feedback signal
- function of the output signal. It is send to the summing point and algebraically added to the reference input signal to obtain the actuating signal.

Actuating signal
- the control action of the control loop and is equal to the algebraic sum of the reference input signal and feedback signal. This is also called the “error signal.”

Manipulated variable
- process acted upon to maintain the plant output(controlled variable) at the desired value.

Disturbance
- undesirable input signal that upset the value of the controlled output of the plant.

CONTROL SYSTEM

Monday, 24 August 2015